개요

SLAM은 filter-based 와 optimization-based 로 편의상 나눌 수 있다.
(물론 두 방법이 robot 의 state 를 추정하는데 상보적으로 동시에 쓰일수도 있다.)

[Factor graph SLAM] 에서는
optimization-based 기반의 SLAM에 대해서 소개하고 있다.

한편, [Filter-based SLAM] 시리즈에서는
filter-based SLAM 에 대해서 소개하려고 하는데,

이 포스트 (와 몇 편 더) 에서는, 그전에
filter-based SLAM의 근간 (mathmatical machinary)이 되는
Bayesian analysis 자체에 대해 먼저 소개하려고 한다.

---

Bayesisan Analysis 란?

Intro

Bayesisan Analysis 이 무엇인지 설명하기 전에,
Bayesisan Analysis 이 왜 필요한지, 예시 상황으로부터 시작해보자.

우리는 어떤 한 시점에서 로봇의 위치를 알고싶다.
이 경우 위치를 $\textbf{x}_{i} = (x, y)$ 의 두 값으로 표현할 수 있다. (heading 은 편의상 생략)

• 상황 1:

  로봇은 위치를 추정하기 위해서 GPS를 사용했다.
  GPS는 로봇의 위치가 $(1,2)$ 라고 알려주었다 (measurement, $\textbf{z}_1$).

  그래서 로봇은 자기의 위치를 $(1,2)$ 이라고 생각하고 여러 미션을 수행하려고 한다.

  근데 GPS는 로봇의 위치가 다시 $(1.5, 3)$ 라고 알려주었다 (measurement 2, $\textbf{z}_2$).
  그래서 로봇은 자기의 위치를 다시 $(1.5, 3)$ 으로 바꿨다.
  근데 GPS는 로봇의 위치가 다시 $(2.5, 1)$ 라고 알려주었다 (measurement 3, $\textbf{z}_3$).
  그래서 로봇은 자기의 위치를 다시 $(2.5, 1)$ 으로 바꿨다.

  … 무한반복 …
  로봇은 확신없이 자기 위치를 결국 추정하지 못하고 결국 세월이 다갔다 …

  이렇게, 매번 개별 measurement만의 가능도 (likelihood) 를 최대화 해주는 방식으로
  위치를 추정하는 게 좋은 방법일까?
  이러면 그때그때 들어오는 measurement 에 biased 된 예측이 내려질 것이다¹.

• 상황 2:

  상황1과 똑같이,
  로봇은 위치를 추정하기 위해서 GPS를 사용했다.
  GPS는 로봇의 위치가 $(1,2)$ 라고 알려주었다 (measurement, $\textbf{z}_1$).

  근데 이 로봇은 자기의 현재 위치가 $(0.5, 2)$ 라고 믿고 있는 상태이다 (prior).
  이 값은 현재 시점에서 측정 (measurement) 한 것은 아니지만 로봇이 알고있는 어떤 믿음이다.
  로봇은 이 경우에도 상황1에서와 같이 현재 측정된 정보만을 최대화 하도록
  자기의 위치를 추정해야할까?

  흠 근데 그건 좀 unreasonable 해 보인다.
  prior 와 measurement 두 정보를 모두 고려하는 게 좋을 것 같다.

  근데 만약 prior 와 measurement 두 정보를 모두 고려한다 하더라도,
  수학적으로 어떻게 융합하여야 하는가?

이에 대답하기 전에 먼저 아주 간단한 수학을 recap하고 넘어가자.

Bayes Rule

Bayesisan Analysis 의 기본 틀은 Bayes Rule 이다.
대학교 확률과 통계 수업을 들으면
거의 첫주에 배우는 아주 기초적이고, 제일 먼저 나오는 내용이라고 할 수 있다.
다들 알다시피 Bayes Rule 을 쓰면 다음과 같다.

\[\begin{align*} p(A \ | \ B) &\propto p(A) \cdot p( B \ | \ A) \\ \end{align*}\]

그런데 robotics (or 여타 estimation 문제) 에서 실제로 중요한 것은
위에서 $A$와 $B$의 위치가 바뀌는게 베이즈어쩌구구나~ 음~ 외웠어~ 가 아니라

$A$와 $B$ 자리에 들어가는 것이,
실 세계에서 어떤 물리적 의미를 지니는지를 이해하는 것이 중요하다.

Bayesisan Analysis 란?

Bayesian analysis 는 우리가 알고싶은 parameter (들, variables as vector)의
posterior probability 를 maximize 하는
optimal parameter (그래서 maximum a posteriori, MAP) 를 찾는 방법을 말한다.

먼 말인지 차근차근 살펴보자.

우리는 시스템의 어떤 상태에 대해 알고 싶다
(예: 로봇의 위치, 로봇의 calibration parameter 등 어떤 것이든.)

이것을 모두 한데 우겨넣고 vector 로 만든 것을 $\textbf{x}$ 라고 해보자 (state).

우리는 $\textbf{x}$ 를 예측하기 위한 단서들을 가지고 있다 (measurements, $\textbf{z}_{1:k}$).
로봇은 센서를 가지고 있기 때문에 다양한 측정을 할 수 있다.
(예: laser 센서로 알려진 랜드마크까지의 거리를 재기, GPS로 위치를 바로 얻기 등)
robotics 에서 measurement 는 문자로 적을 때는 $\textbf{z}$ 로 많이 적는 편이다.

따라서 우리가 관심있는 SLAM (i.e., state estimation) 이란 문제는,
로봇이 가진 센서를 이용해서 얻은 다양한 측정값이 주어졌을 때 (given),
$\textbf{x}$ 를 추론하는 문제이다 (inference).

이를 수학적으로 표현하면 $p ( \textbf{x} \ | \ \textbf{z}_{1:k} )$ 로 쓸 수 있다 ².

따라서 SLAM (state estimation)이란 무엇인가?
수학적으로:
$\textbf{z}$가 given 일 때
$\textbf{x}$의 확률이 최대가 되는 $\textbf{x}$ 값을 구하는 것이다.

그런데, Practically, 공학적으로는 어지간하면
우리는 관심있는 random variable 들 ($\textbf{x}$ 등)이
모두 Gaussian 이라고 가정한다.
Gaussian 분포는 여러가지 유용한 성질이 있기 때문이다 (후술함). $+\alpha$³

암튼 우리가 최대화하려는 이 확률 $p ( \textbf{x} \ | \ \textbf{z}_{1:k} )$ 은
measurement 가 측정이 완료되어서, 주어져야 계산할 수 있기 때문에
사후확률 (posterior) 이라고 부른다.

그런데 이 posterior는 Bayes rule 에 의해,
다음과 같이 두개의 텀으로 분리가 되고, 각각을 prior 와 likelihood 라고 부른다.

\[\begin{align*} p(\textbf{x} \ | \ \textbf{z}_{1:k}) &\propto p(\textbf{x}) \cdot p(\textbf{z}_{1:k} \ | \ \textbf{x}) \\ \text{posterior} &\propto \text{prior} \cdot \text{likelihood} \end{align*}\]

$\propto$ 로 쓴 이유: 보통 분모는 normalization 용도 (확률의 정의를 지켜주기 위해서 sum 을 1로 만들어주는 역할)로 생각되기 때문에, 통상적으로 practically 생략하는 편이 많다. 어짜피 우리가 관심이 있는 것은 최대확률값이 아니라, 최대확률이 될 때의 $\textbf{x}$값이기 때문이다 (상수의 곱에 무관하다).

이 때 일반적으로 우리는 prior 와 likelihood 가 Gaussian 을 따른다고 가정한다.
그러면 Gaussian 의 좋은(!) 성질 덕분에 posterior 도 Gaussian이 된다.

여기서 그럼 다시 물어야 할 것이,
posterior가 Gaussian인 것이 (state estimation 관점에서) 왜 중요할까?

• 일단 Gaussian은 optimal argmax 값을 얻기가 편하다 (median이 mean 과 같음) ⁴.
• 그리고 Gaussian인 경우, 자연스럽게 recursive 한 estimation 이 가능해진다. 이게 뭔말이냐면, 현재 턴의 posterior 가 다음턴의 prior 로 쓰인다고 생각해보자. 앞서, 우리는 prior 가 Gaussian이라고 가정했었다. 그럼 posterior 도 Gaussian이 되고, 다음턴의 prior 도 다시 Gaussian이 되고, 그 턴의 posterior 도 다시 Gaussian이 되고, … 무한 반복.⁵
  • 즉, 현재 시점에서 얻은 사전 정보를 다음턴에 자연스럽게 활용할 수 있다. 심지어 가우시안의 유용한 성질들 덕분에 그 recursive update 조차도 closed form 으로 딱 떨어진다 (곧 증명해본다).
• 또한, Gaussian은 mean (optimal) 과 더불어 covariance (uncertainty) 도 얻을 수 있다.
  • 예를 들어 앞서 본 예시상황2 에서 prior 와 likelihood 를 어떻게 융합해야하는지에 관한 문제가 있었다. 이 비율의 balancing 이 prior 와 likelihood 각각의 uncertainty 들에 의해 조절된다 (곧 증명해본다)!
  • robotics 는 거의 uncertainty 에 관한 학문이라고 할 수 있을만큼 이 uncertainty 는 다양하게 쓰이고 중요하다 ⁶.

암튼 정리해보자면

우리가 state estimation 에서 Bayesian filtering 이라고 부르는 것은 다음과 같은 상황을 의미한다.

• 로봇은 자신의 상태 (state) $\textbf{x}$의 최적값을 알고 싶다 ⁷.
  • 어떤 물리적 (위치, 속도 등) 혹은 비물리적 (임의의 시스템 파라미터) 요소라도 state 가 될 수 있다. 가장 일반적으로는 pose (e.g., SE(3)).
• 로봇은 센서측정데이터 (measurement) $\textbf{z}_{1:k}$ 를 가지고 있다.
  • 어떤 센서라도 가능하다. 가장 일반적인 것은 Camera, LiDAR, IMU, GPS, Radar, Wheel encoder 등.
• 우리는 $ p(\textbf{x} \ | \ \textbf{z}_{1:k}) $ 를 최대화 하고 싶다 ².
  • $==$ 우리는 posterior probability 의 mean (== 확률을 최대로 하는 $\textbf{x}$) 과 covariance 를 알고 싶다.
• 우리는 posterior 를 직접 최대화하는 것이 아니라, 대신 우회적으로 prior 와 likelihood 의 곱을 최대화 한다.
• prior 와 likelihood의 분포로 Gaussian 을 사용한다.
• covariance는 pior 와 likelihood 를 융합할 때 기여도를 고려하는 역할을 한다.

• posterior의 mean 과 covariance는 prior 와 likelihood 의 mean 과 covariance 를 이용해서 (closed-form으로!) 얻어진다 (이제 증명해 봄)
• posterior 는 다음 턴의 prior 로써 기능 ⁸ 한다.
  • 다음 편 (Bayesian Filtering 이야기 (2편)) 에서 더 자세히 다룰 예정.

---

Posterior 의 mean, covariance 구하기

이번 포스팅에서 원래 하려고했던 걸 이제야 (…) 소개한다.

앞서 우리는, 우리가 알고싶어하는 값 $\textbf{x}$ 의 posterior probability 의
mean 과 covariance 를 알고싶어한다고 소개했다.

이것이 사실 Filter-based SLAM의 수학적 틀 ⁹ 이기도 하다!

왜 mean 이 궁금한 것인가에 대해 다시 한번 recap을 하자면,
Gaussian일 경우, 그 값이 posterior probability 를 최대화해주는 값이기 때문이다.
확률이 최대란 말은, 확률이 최대가 되는 그 때의 $\textbf{x}$ 가 말 그대로 가장 “probable” 하다는 뜻이 된다.

또한, posterior probability 의 mean 과 covariance 는
prior 와 likelihood 의 mean 과 covariance 들을 이용해서 얻어진다고 소개 했었다.

여기서 먼저 두괄식으로 공식 만 소개하자면 다음과 같다.

\[\begin{align*} \Sigma_{\text{posterior}} &= ( \Sigma_{\text{prior}}^{-1} + \Sigma_{\text{likelihood}}^{-1})^{-1} \\ \mu_{\text{posterior}} &= \Sigma_{\text{posterior}}(\Sigma_{\text{prior}}^{-1} \mu_{\text{prior}} + \Sigma_{\text{likelihood}}^{-1} \mu_{\text{likelihood}}) \end{align*}\]

암튼 그래서 우리는 posterior 의 mean 과 cov를 구하기 위한 building block으로써
먼저 prior 와 likelihood 의 mean 과 covariance 에 대해 알아보아야 한다.
(위의 식에 대입해서 풀어나가면 된다)

prior 에는 random variable 이 $\textbf{x}$ 하나밖에 없기 때문에,
간단하게 그냥 mean 과 covariance 를 말해줄 수 있다.
$\textbf{x}$ 의 mean 을 $\textbf{m}_0$, covariance 를 $\textbf{P}_0$ 라고 하면 된다.
subscriptor 로 $0$를 쓴 이유는 별 이유는 없고 그냥 시작 시점이다~ 최초의 시점이다~ 그런의미이다.

그럼 likelihood 의 mean 과 covariance 는 무엇일까? 알아보자.

Measurement Model

likelihood는 $p(\textbf{z}_{1:k} | \ \textbf{x})$ 이거였다.

여기서는 총 $k$ 개의 측정 값을 모두 이용한다는 상황인데,
제일 간단하게 하나의 측정 $\textbf{z}_{i}$만을 생각해보자.

이 때, 각 측정이 모두 독립적이라면,
다음과 같이 likelihood는 개별 measurement 들의 확률의 총 곱이된다.

$p(\textbf{z}_{1:k} | \ \textbf{x}) = \prod_{i = 1}^{k} p(\textbf{z}_{i} | \ \textbf{x})$

그럼 다시 질문은
a single measurement ($p(\textbf{z}_{i} | \ \textbf{x})$) 의 mean 과 covariance 는 무엇일까? 라는 질문이 된다.

식에서 알수있듯이, $p(\textbf{z}_{i} | \ \textbf{x})$ 에서는
$\textbf{x}$가 알려진 값 (given) 역할이며
$\textbf{z}_i$ 는 알고싶은 (모르는) variable 이다.

따라서 $\textbf{x}$ 가 input (given) 이고 $\textbf{z}_i$ 가 output 인 어떤 함수를 생각해볼 수 있다.

보통 그 함수를 measurement model 이라고 부르고 $h$ 로 많이 적는다.
식으로 적으면 $\textbf{z}_i = {h}_{i}(\textbf{x})$ 가 된다.

예를 들어 1차원 선상에서 움직이는 로봇을 생각해보자.
어떤 알려진 landmark 가 $2$ 의 위치에 있었다고 하자 ($2$의 위치에 있다는 사실도 로봇에게 알려져있다¹⁰).

이 때 로봇은 거리센서를 가지고 있어서 그 landmark 까지의 거리를 잴 수 있다.
그럼 그 거리측량값 (measurement) $\textbf{z}_i$ 는, 로봇의 위치에 의존적일 것이다.

예를 들어, 여기서는
$\hat{\textbf{z}_i} = h_i(\textbf{x}) = | \textbf{x} - 2 |$ 가 될 것이다.

이렇듯 우리는 “실측” 하기 전부터,
현재 state 를 이용해서, 그 실측값이 어떤 값일지를 미리 “예측” 해볼 수 있다.
이것이 바로 measurement model 이다.
($\hat{}$ 은 예측 (estimated) 값 이라는 의미이다)

즉, $h_i(\cdot)$는 $\hat{\textbf{z}_{}}$ 와 $\textbf{x}$ 를 mapping 해주는 함수 라고 말할 수 있다.

그런데 이 때, 일반적으로,
공학적으로 계산상의 이점을 얻기 위해서는 (Linear algebra 의 다양한 툴들을 활용하기 위해서는),
그 mapping 함수가 linear 할 필요가 있다 (== matrix 곱으로 표현될 수 있어야 한다).

위의 예시에서는 measurement model 이 $| \textbf{x} - 2 |$ 와 같이 간단한 함수였지만
다양한 센서를 사용하다보면 exponential, cosine, 등이 다 섞이는 nonlinear 한 함수가 될 때도 있다.

이 경우, linear 하지 않기 때문에 (matrix 곱으로 나타낼 수 없기 때문에),
우리는 (일반적으로) nonlinear (라고 가정하는) 인 measurement model 을 미분해서 matrix 로 만들어준다.

이것이 흔히들 “자코비안” 이라고 부르는 것이며,
자세한 수학적 근거는 대학미적분학 정도를 들었다면 다 알것이므로 생략한다.
혹은 여기를 참고: vector-by-vector 미분 (위키)

$h(\cdot)$ 을 미분해서 선형화 시킨 것 (i.e., $h(\cdot)$의 자코비안) 을
보통 $H$ 와 같이 대문자로 많이 적는다.

이 경우 linear 하므로, $h(\textbf{x})$ 에서처럼 괄호 안에 argument 방식으로 굳이 적어줄 필요가 없어진다.
즉, $\hat{\textbf{z}_{}} = H_i\textbf{x}$ 와 같이 간단히 매트릭스 곱으로 적을 수 있다.

근데 이것은 실측 값이 아니라 예측값 (말 그대로 “모델”)임을 잊지 말아야 한다!

실측값은 센서 오차 등으로 $H_i\textbf{x}$ 와는 조금 다를 수 있다.
$H_i\textbf{x}$ 에 여기에 또 Gaussian noise 가 더해진 것이 실측값 $\textbf{z}$ 라고 모델링 해볼 수 있다.
이 noise 는 말 그대로 noise 이기 때문에 mean 이 $0$ 이고 covariance 가 대충 작은 값 얼마라고 할 수 있다 ¹¹.

문제를 단순화 하기 위해서
$\textbf{z}_i$ 가 1-dim vector 이고
따라서 a single measurement 의 covariance 가 단순히 어떤 스칼라 값 $\sigma^{2}$ 라고 하자 (이후 포스팅에서 일반화해봄).

그럼 noise 의 mean 은 0이었기 때문에
실제 measurement $\textbf{z}_{i}$ 는
mean이 $H\textbf{x}$ 이고, variance 가 $\sigma^{2}$ 인 Gaussian 을 따른다고 말할 수 있다.

이를 $p(\textbf{z}_{i} | \ \textbf{x}) = \mathcal{N}(H_i\textbf{x},\sigma^{2}) $ 라고 표현할 수 있다.

거의 다왔다.

이제 prior 와 likelihood 의 mean 과 covariance 들이 모두 준비되었다.
이거를 어떻게 잘 융합하면 posterior 의 mean 과 covariance 가 나오는지 이제 유도해보자.

Gaussian 의 성질

Gaussian 분포는 이런 성질(장점) 들을 가지고 있다. ( 출처 )

여기서 네번째 성질을 이용하려고 한다.

다음과 같다.

저기 중앙의 수식에 적힌대로 따라 하면 된다.
차근 차근 해보자.

Posterior 의 mean 과 covariance 유도

이해하기 쉽도록 위의 그림에 있는 수식 과 같은 notation 을 사용하자.

번호 $1$ 의 위치에 prior, 번호 $2$ 번의 위치에 likelihood 를 넣어보자.
그러면 일단 prior 에 대해서는 쉽다¹²:

\[\begin{align*} \Sigma_{1} &= \textbf{P}_0 ,\\ \mu_{1} &= \textbf{m}_0 \end{align*}\]

그럼, likelihood에 대한, $\Sigma_{2}$ 와 $\mu_{2}$는 무엇인가?

일단, likelihood 가 $\prod_{i = 1}^{k} p(\textbf{z}_{i} | \ \textbf{x})$ 처럼 여러개의 항들의 곱이었기 때문에 위의 공식을 이용하려면 하나의 항으로 만들어 주어야 한다.

이를 위해서 $\textbf{z}_i$ 들을 쌓아서 하나의 긴 vector $\textbf{z}$ 를 만들어 주자.

그러면 $\textbf{z}$는 mean 이 $\textbf{H}\textbf{x}$ 이고 covariance 가 diag($\sigma^2$) $=\sigma^2 \textbf{I}$인¹³ Gaussian을 따르게 된다.

이 때 $\textbf{H}$ 는 $\textbf{H}_i$ 를 세로로 쌓은 (stack) matrix 이다.
$\textbf{I}$는 identity matrix 이며 shape 은 $\textbf{H}$의 세로(row)길이 by 세로길이 가 된다.

이를 $p(\textbf{z} | \textbf{x}) = \mathcal{N}(H\textbf{x},\sigma^{2}\textbf{I}) $ 라고 표현할 수 있다.

그럼 이제 $\Sigma_{2}$ 와 $\mu_{2}$ 로써, $\textbf{H}\textbf{x}$ 와 $\sigma^{2}\textbf{I}$를 쓰면 되나?

안된다!

$\textbf{H}\textbf{x}$ 와 $\sigma^{2}$ 는 “$\textbf{z}$” 의 mean/cov 이기 때문이다.

위의 그림에 있는 수식 을 이용하려면
$\Sigma_{2}$ 와 $\mu_{2}$ 는 “$\textbf{x}$” 의 mean/cov 여야 한다.
(prior 도 $\textbf{x}$ 에 대한 것이고, 우리가 관심있는 posterior 도 $\textbf{x}$에 대한 것이기 때문이다.)

우리는 $\textbf{z}$ 의 mean/cov 를 알고 있는데,
이를 이용해서 $\textbf{x}$ 의 mean/cov 를 알 수 있다.

Gaussian 의 exponential term 을 요리조리 재구성하면 그것을 얻을 수 있다.

먼저 Gaussian 분포의 실제 수식 생김새를 보면, 이렇게 생겼다.

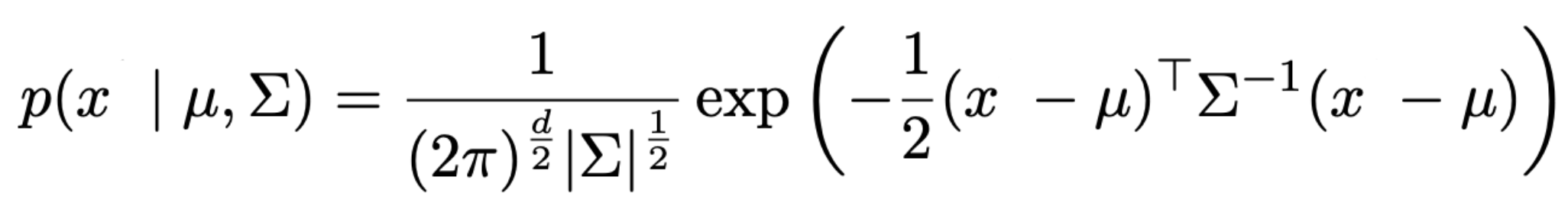
여기서 exponential 안쪽의 각 항에 위치하는 애들이 mean 과 covariance 의 의미를 가진다.

즉, 회색 dotted box 안의 값만 중요하다.
(아까부터 계속 말했듯 exp 바깥의 term 들은 상수로써 확률의 합을 1로 만들어 주기 위함이고, 확률을 최대화 하는 argmin (i.e., mean) 에는 영향을 주지 않는다)

까만 박스 위치에 놓이는 것이 우리가 관심있는 random variable 이다.
파란 박스 위치에 놓이는 것이 그 random variable 의 mean 이다.
빨간 박스 위치에 놓이는 것이 그 random variable 의 covariance 이다.

그럼 이 때, 지금 우리의 경우에서는: 즉, $p(\textbf{z} | \textbf{x})$ = $\mathcal{N}(H\textbf{x},\sigma^{2}\textbf{I}) $ 일 때,
$p(\textbf{z} | \textbf{x})$ 의 exponential term 은 이렇게 생겼을 것이다 (-1/2 도 편의상 생략).

\[\begin{align*} ( \textbf{z} - \textbf{H}\textbf{x} )^{T} (\sigma^2 \textbf{I})^{-1} ( \textbf{z} - \textbf{H}\textbf{x} ) \end{align*}\]

좀 전에 말했듯 까만 박스 위치에 지금은 $\textbf{z}$ 가 놓여있다.
근데 우리의 관심사는 $\textbf{x}$ 의 mean과 covariance 이다.

따라서 위의 수식의 모양새를 수정해서 (하지만 수식 자체가 바뀌면 안된다 (동치여야 한다))

지금 $\textbf{z}$ 가 있는 위치에 $\textbf{x}$가 놓이도록 수정해보자.

$(\textbf{H}\textbf{H}^{T})(\textbf{H}\textbf{H}^{T})^{-1}$ 가 $\textbf{I}$ 와 같다는 사실 (자명하다) 을 이용해보자

\[\begin{align*} & ( \textbf{z} - \textbf{H}\textbf{x} )^{T} (\sigma^2 \textbf{I})^{-1} ( \textbf{z} - \textbf{H}\textbf{x} ) \\ = \ & ( \textbf{I}\textbf{z} - \textbf{H}\textbf{x} )^{T} (\sigma^2 \textbf{I})^{-1} ( \textbf{I}\textbf{z} - \textbf{H}\textbf{x} ) \\ = \ & \left( (\textbf{H}\textbf{H}^{T})(\textbf{H}\textbf{H}^{T})^{-1}\textbf{z} - \textbf{H}\textbf{x} \right)^{T} (\sigma^2 \textbf{I})^{-1} \left( (\textbf{H}\textbf{H}^{T})(\textbf{H}\textbf{H}^{T})^{-1}\textbf{z} - \textbf{H}\textbf{x} \right) \\ = \ & \left( \textbf{H}(\textbf{H}^{T})(\textbf{H}\textbf{H}^{T})^{-1}\textbf{z} - \textbf{H}\textbf{x} \right)^{T} (\sigma^2 \textbf{I})^{-1} \left( \textbf{H}(\textbf{H}^{T})(\textbf{H}\textbf{H}^{T})^{-1}\textbf{z} - \textbf{H}\textbf{x} \right) \\ = \ & \left( \textbf{H} \left( \textbf{H}^{T}(\textbf{H}\textbf{H}^{T})^{-1}\textbf{z} - \textbf{x} \right) \right)^{T} (\sigma^2 \textbf{I})^{-1} \left( \textbf{H} \left( \textbf{H}^{T}(\textbf{H}\textbf{H}^{T})^{-1}\textbf{z} - \textbf{x} \right) \right)\\ = \ & \left(\left( \textbf{H}^{T}(\textbf{H}\textbf{H}^{T})^{-1}\textbf{z} - \textbf{x} \right)^{T} \textbf{H}^{T} \right)(\sigma^2 \textbf{I})^{-1} \left( \textbf{H} \left( \textbf{H}^{T}(\textbf{H}\textbf{H}^{T})^{-1}\textbf{z} - \textbf{x} \right) \right) \\ = \ & \left( \textbf{H}^{T}(\textbf{H}\textbf{H}^{T})^{-1}\textbf{z} - \textbf{x} \right)^{T} \left( \textbf{H}^{T} (\sigma^2 \textbf{I})^{-1} \textbf{H} \right) \left( \textbf{H}^{T}(\textbf{H}\textbf{H}^{T})^{-1}\textbf{z} - \textbf{x} \right) \\ = \ & \left( \textbf{x} - \textbf{H}^{T}(\textbf{H}\textbf{H}^{T})^{-1}\textbf{z} \right)^{T} \left( \frac{\textbf{H}^{T}\textbf{H}}{\sigma^2} \right) \left( \textbf{x} - \textbf{H}^{T}(\textbf{H}\textbf{H}^{T})^{-1}\textbf{z} \right) \\ = \ & \left( \textbf{x} - \mu_{x} \right)^{T} \left( \Sigma_{x}^{-1} \right) \left( \textbf{x} - \mu_{x} \right) \end{align*}\]

해설¹⁴

따라서 우리는 이로부터,
$\textbf{H}\textbf{x}$ 와 $\sigma^{2}$ 가 각각 $\textbf{z}$ 의 mean 과 covariance 일 때,
$\textbf{x}$ 의 mean은 $\textbf{H}^{T}(\textbf{H}\textbf{H}^{T})^{-1}\textbf{z}$ 이고, covariance 는 $\left( \frac{\textbf{H}^{T}\textbf{H}}{\sigma^2} \right) ^{-1}$ 임을 알 수 있다.
(NOTE: 여기서 $\textbf{z}$ 는 로봇이 센서를 이용해서 실측한 값이다)

따라서 위의 그림에 있는 수식 의 $\Sigma_{2}$ 와 $\mu_{2}$ 는 다음과 같다.

\[\begin{align*} \Sigma_{2} &= \left( \frac{1}{\sigma^2}\textbf{H}^{T}\textbf{H} \right) ^{-1} ,\\ \mu_{2} &= \textbf{H}^{T}(\textbf{H}\textbf{H}^{T})^{-1}\textbf{z} \end{align*}\]

따라서 Gaussian product 의 공식대로 하면
posterior 의 mean 과 covariannce 는 다음과 같다.

먼저 posterior 의 covariance $\textbf{P}_{\text{pos}}$는 다음과 같다. (슬라이드 그림에서 $\Sigma$ 로 되어있어서 지금까지 $\Sigma$ 로 이야기했는데, covariance 를 일컫는 notation 을 prior 에서 그랬듯이 $\textbf{P}$ 로 다시 통일하도록 하자)

\[\begin{align*} \textbf{P}_{\text{pos}} &= \left( \Sigma_1{}^{-1} + \Sigma_2{}^{-1} \right)^{-1} \\ &= \left(\textbf{P}_0^{-1} + \frac{1}{\sigma^2}\textbf{H}^{T}\textbf{H} \right)^{-1} \end{align*}\]

그리고 posterior 의 mean $\textbf{m}_{\text{pos}}$ 는 다음과 같다.

\[\begin{align*} \textbf{m}_{\text{pos}} &= \textbf{P}_{\text{pos}} \left( \Sigma_1{}^{-1}\mu_{1} + \Sigma_2{}^{-1}\mu_{2} \right) \\ &= \textbf{P}_{\text{pos}} \left( \textbf{P}_0^{-1} \textbf{m}_0 + \left( \frac{1}{\sigma^2}\textbf{H}^{T}\textbf{H} \right) \left( \textbf{H}^{T}(\textbf{H}\textbf{H}^{T})^{-1}\textbf{z} \right) \right) \\ &= \textbf{P}_{\text{pos}} \left( \textbf{P}_0^{-1} \textbf{m}_0 + \left( \frac{1}{\sigma^2}\textbf{H}^{T} \right) \left( \textbf{H} \textbf{H}^{T} \right) (\textbf{H}\textbf{H}^{T})^{-1}\textbf{z} \right) \\ &= \textbf{P}_{\text{pos}} \left( \textbf{P}_0^{-1} \textbf{m}_0 + \frac{1}{\sigma^2}\textbf{H}^{T}\textbf{z} \right) \\ &= \left(\textbf{P}_0^{-1} + \frac{1}{\sigma^2}\textbf{H}^{T}\textbf{H} \right)^{-1} \left( \textbf{P}_0^{-1} \textbf{m}_0 + \frac{1}{\sigma^2}\textbf{H}^{T}\textbf{z} \right) \end{align*}\]

증명 끝!

이를 수식으로 다시 정리하면:

\[\begin{align*} p(\textbf{x} | \textbf{z}) = \mathcal{N} \left(\left(\textbf{P}_0^{-1} + \frac{1}{\sigma^2}\textbf{H}^{T}\textbf{H} \right)^{-1} \left( \textbf{P}_0^{-1} \textbf{m}_0 + \frac{1}{\sigma^2}\textbf{H}^{T}\textbf{z} \right), \ \ \left(\textbf{P}_0^{-1} + \frac{1}{\sigma^2}\textbf{H}^{T}\textbf{H} \right)^{-1} \right) \end{align*}\]

가 된다!

결과만 보면 좀 복잡해보이지만, 이 식이 유도되어온 맥락 을 기억한다면
그리 어렵게 느껴지진 않을 것 같다!

---

요약

• Bayesian Filtering 의 뿌리에 대해 알아보았습니다.
  • posterior 는 measurement 가 주어졌을 때, state 의 확률을 의미한다. 그리고 이것을 최대화하는 과정을 MAP (maximum a posteriori) 라고 부른다.
  • 실제로는 posterior 의 mean 과 covariance 를 직접 구하지 않고, prior 와 likelihood 의 mean 과 covariance 를 조합해서 구한다.
  • prior, likelihood, posterior 가 모두 Gaussian이라고 가정할 경우, Gaussian product 에 의해, posterior 의 mean 과 covariance 가 closed form 으로 딱 떨어진다.
  • 그리고 이렇게 얻어진 posterior는 다음 턴의 (새로운 measurement 가 하나 더 들어왔다고 생각해보자) prior 로 다시 쓰인다. 즉, recursive estimation 이 가능한 수학적 엔진을 오늘 만들어보았다! (recursive estimation 에 대해서는 다음편에서 더 자세히 이야기함)
• Bayesian Filtering 공부에 대해서, 이 책¹⁵을 추천합니다

---

예고

• 다음 편에서 오늘 유도한 걸 그대로 이용해서 칼만필터를 유도해보겠습니다.

---

주석

Other posts

• [SLAM Study] » Gauss-Newton Opt == IEKF update ?
• [SLAM Study] » SLAM Back-end 공부자료 5개 추천
• [Radar SLAM] » ICRA 2021 Radar in Robotics Workshop 요약
• [Radar SLAM] » Radar Odometry Results on MulRan dataset
• [LiDAR SLAM] » Scan Context-based LiDAR Pose-graph SLAM [구현]
• [Visual SLAM] » Filter-based VIO [1편] — MSCKF 계열 history 정리
• [Least Square Opt.] » Iterative Optimization [1편] — Nonlinear ICP 구현을 통해 알아보는 Gauss-newton Optimization
• [Filter-based SLAM] » Bayesian Filtering [2편] — Recursive estimation 의 시작 (칼만필터 유도)
• [Factor graph SLAM] » SLAM back-end [2++편] — Householder QR 분해 구현해보기
• [Factor graph SLAM] » SLAM back-end [2편] — Ax=b 대신 Ry=d 를 풀자