-->


[Factor graph SLAM] ― March 04, 2021

SLAM back-end [1편] — SLAM은 Ax=b 를 푸는 것이다

개요

SLAM은 세상의 모든것 [1. 나 (robot)와 2.너 (world)] 의
state (e.g., position, orientation, velocity) 를 예측하는 학문이다.
그래서 state estimation 이라고 불리기도 한다.

이런 최적 state 를 예측하는 solver 에 관한 연구를
SLAM back-end 라고 편의상 부르기도 한다.

그런데 어떻게 예측할까? 어떻게 최적해를 얻을까?

(SLAM back-end의 마일스톤 논문인) Square Root SAM 논문1 에서 말했듯,
SLAM은 수학적으로 $Ax=b$ 를 푸는 문제이다.

그래서 SLAM back-end 라고 하면 주로

어떻게 더 $Ax=b$를
빠르고 (fast), 정확하고 (accurate), 안정적으로 (numerically stable) 풀 수 있는지에 대한 연구라고 생각하면 된다.

(다음 편들에서 그런 알고리즘들에 대해서 자세히 알아보도록 하고)

일단 왜 SLAM이 $Ax=b$ 를 푸는 문제인지 알아보자.

SLAM 이란

어느 마을에 건설로봇 (SCV)이 있었다.

얘는 자기가 어디서 온 지 모른다.

그래서 편의상 자기가 현재 Origin (e.g., [0, 0]) 에 있다고 생각한다.

img1

SCV는 길을 가고 있었다. 로봇인 이상 움직이지 않을 수 없으므로.

img2

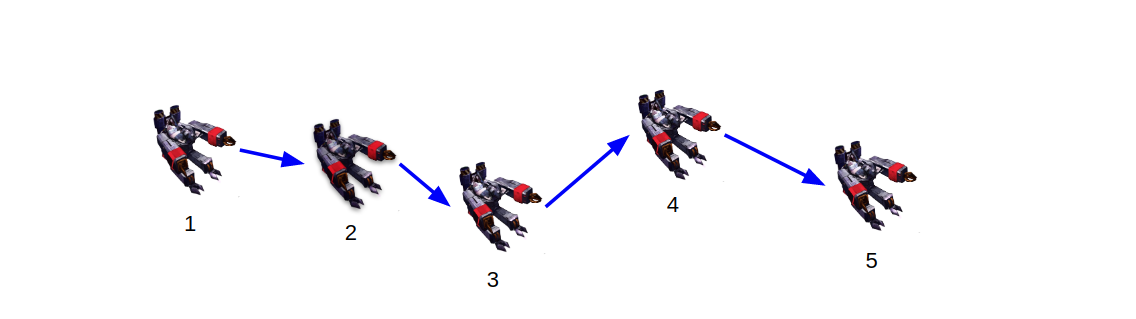
얘는 사이사이마다 얼마만큼 이동한지 (relative motion) 를 측정하는 능력 (odometry) 이 있어서 (파랑 화살표),

자연스럽게 $t=2, 3, 4, 5$에서의 위치도 계산할 수 있었다 (localization).

근데 그 능력 (odometry) 은 엄청 정확하지는 않아서 (sensor noise),
갈수록 자기가 어디에 있는지 덜 신뢰하게 될 수밖에 없었다 (uncertainty was propagated).

그래서 얘는 주변의 포토캐논들 (landmark) 을 봐가면서 이동하기 시작했다.
SCV는 사실 laser 를 장착하고 있어서 포토캐논까지의 거리를 직접적으로 잴 수 있었다 (주황 화살표).

img3
Figure: Bayes Net

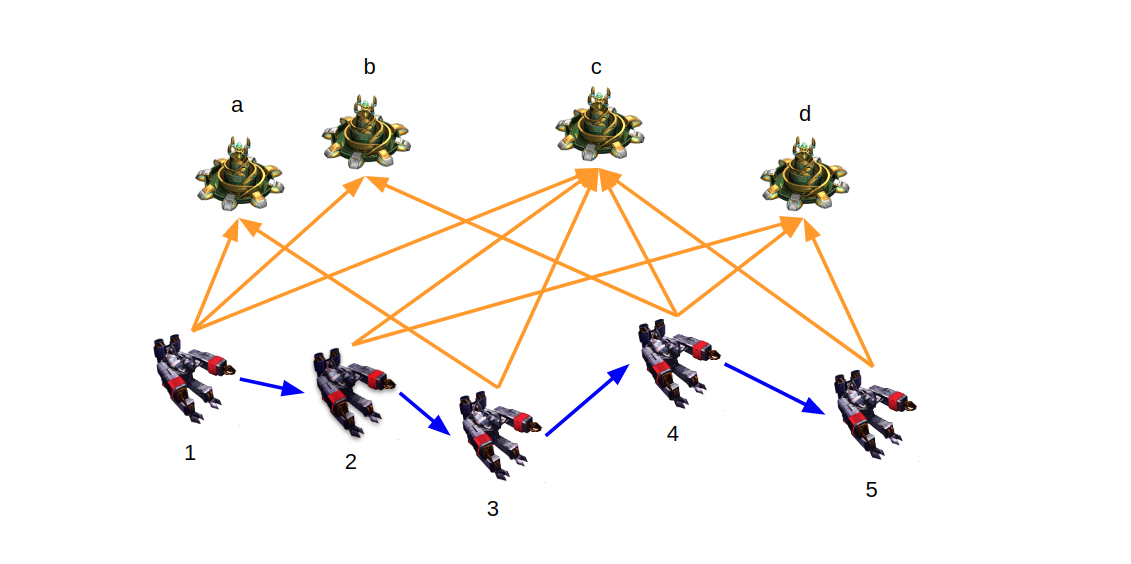
그래서 파랑색 제약 (motion constraints) 도 다 만족시키는 와중에,
노란색 제약 (landmark constraints) 들도 다 만족시키도록 한다면
SCV는 자기의 위치를 조금 더 정확히 추정할 수 있을 것이다.

통상적으로 파랑색 제약을 생성하는 모델을 motion model,
노란색 제약을 생성하는 모델을 observation model 이라고 부르긴 하는데
그냥 여기서는 둘 다 measurement (or factor) 라고 부르자.

이런 관계 (방향성, directed) 그래프를 Bayes Net 이라고 부른다.
(ps. Bayes Net에 관한 좋은 강의 추천2)

근데 우리는 그림이 필요한게 아니라 (iSAM2에 가면 필요하다. 언젠가 다음편에서 소개함3),
Algebraically 풀 수 있는, 즉 대수적인 툴이 필요하기 때문에
이 Bayes Net의 measurement 들을 한 데 다 우겨넣으면

이렇게 matrix 형태로 표현할 수 있다.

img4
Figure: SLAM system

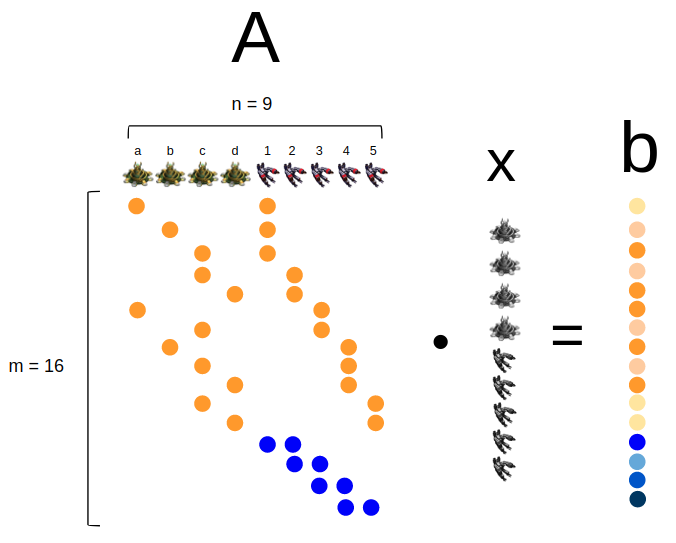
SCV는 구비한 sensor (laser 등)들과 motion model 과 observation model 을 통해 $\textbf{b}$ 를 직접 측정해서 알고 있다.

따라서 SCV의 정교한 위치(state) 는
위의 $Ax=b$ 를 풀어서 나오는 최적해일 것이다 (state estimation).

덤으로 포토캐논들의 위치도 알 수 있게 된다 (mapping) 개이득.

우리는 여기서 통상적인 사실 몇 가지를 알 수 있다.

  • matrix $A$는 $m \times n$의 형태인데 통상적으로 $m$이 $n$보다 크다는 것이다 ($m > n$). 이런 상황을 보고 overdetermined system 이라고 부른다. ps. 심화과정4
  • matrix $A$는 sparse 하다. 왜냐하면 하나의 measurement 는 적은 수의 entity들 사이의 관계만 규정하기 때문이다 (여기서는 두개 사이의 관계들만 예시로 나오고 있지만 물론 당연히 둘 이상일 수 있다. ps. 심화과정5).

SLAM이란 도대체 무엇인가?

이제는 명확해졌다!

SCV는 이 연립방정식 $Ax=b$를 풀어야 한다!!!

어떻게 Ax=b를 풀까?

$Ax=b$를 풀 때, A의 inverse (혹은 pseudo inverse) 를 곱해서 바로 (deterministic) $x$ 를 쉽게 구할 수 있지~ (normal equation 이라고 부른다)
라고 말한다면 그것은 중학교 교과서에서만 가능한 연립방정식 예제에 불과하다…

실제로는 SCV의 odometry와 laser sensor 가
정확하지 않기 때문에 (noisy measurements) SCV는 싼 유닛이다

해 (optimal solution) 가 deterministic 하게 존재하지 않을 수 있다.
즉, 완전히 $Ax == b$ 로 완벽히 같을 수는 없다는 말.

대신 우리는 $ |Ax - b|_{2}^{2} $ 를 최소화하는 해를 찾게 된다 (least square optimization6).
완벽히 같진 않더라도 비슷은 해지자고.

이 경우 거의 iterative 하게 푸는 것이 국룰이다.
즉, optimal 한 $x^{*}$ 를 단번에 찾을 수는 없고, 대신,

  1. $x_{0}$으로부터 출발해서 optimal 한 변화량 $\Delta^{*}$ 을 추정한다음에
  2. $x_{\text{next}} = x_{\text{prev}} + \Delta^{*} $ 만큼 업데이트 해주는 방식으로 최적해를 향해 나아간다.

그러면 어떻게 $Ax=b$ 를 풀까? 라는 문제는

다시, 어떻게 $A\Delta=b$ 를 풀까? 라는 문제가 된다 7.

따라서 SLAM이란, $\underset{\Delta}{\mathrm{argmin}} \ ||A\Delta - b ||_{2}^{2}$ 인 $\Delta$를
어떻게 (효율적으로 w.r.t time and memory) 찾을까? 에 대답하는 문제이다.


*** 다음 시간에 계속 ... ***


요약

  • SLAM back-end 입문으로 Factor graphs for robot perception 책 8 을 추천합니다. SAM, iSAM, iSAM2 세 논문의 내용을 쉬운 언어로 잘 서술하고 있습니다.

ps. 심화과정 – 팩트체크: 근데 사실 b는 … 9

예고

다음으로

SLAM back-end 이야기 (2편): $Ax=b$ 풀기
— QR decomposition 이란? + Householder reflection 구현 (Matlab 실습)

편을 써보겠습니다.

그 다음으로 제발 <SLAM back-end 이야기 (2편): $Ax=b$ 풀기 — Householder reflection 이론> 편을 써보겠습니다.

생각해보기

  1. SCV의 SLAM system matrix 에서 지금 matrix 의 column 순서가 포토캐논부터 적혀져있다. 근데 이거를 SCV부터 적으면, 즉 column order 가 달라지면 estimation 할 때 어떤 점들이 달라질까? 해가 달라질까? 더 빨리 풀 수 있을까? 아니면 아무 상관 없을까?

  2. SCV 는 $t=3$에서 포토캐논 a 와 c를 봤다고 생각했다. 하지만 알고보니 b와 d를 본 것이었다면? 즉 data association 의 outlier 가 존재할 때 SLAM 의 최적해는 어떤 영향을 받을까? 그리고 이런 false association 이 존재함에도 불구하고, 어떻게 해를 더 강건하게 예측할 수 있을까?

  3. $||Ax - b ||_{2}^{2}$ 의 argmin 을 찾는 것은 일반적으로 SLAM외에도 다른 computer vision estimation 문제에도 매우 자주 등장하는 상황이다. SLAM에 있어 위 식을 푸는 것은 다른 computer vision 의 estimation 문제와 어떤점에서 특별하게 다를까?

주석

  1. Dellaert, Frank, and Michael Kaess. “Square Root SAM: Simultaneous localization and mapping via square root information smoothing.” The International Journal of Robotics Research 25.12 (2006): 1181-1203. ↩

  2. Youtube lectures — Factor graphs short course (Jan 2020, UAL) by Prof. Jose Luis Blanco ↩

  3. (1) 실제로는 랜드마크 수가 훨씬 더 수백 수천개만큼 많을 수도 있고 (SfM), 없을 수도 있다 (Pose-graph SLAM)
    (2) 실제로는 measurement model들이 대부분 non-linear 하기 때문에 1차미분한 Jacobian matrix H가 쓰인다. 더 엄밀하게는 이 H에 covariance matrix (noise matrix) 의 inverse squared 가 곱해진 형태가 A이다. 자세한 것은 이 책8의 chapter 2 를 참고.
    (3) 최근에는 underdetermined system 일 때 SLAM을 어떻게 풀어야할지에 관한 연구도 이루어지고 있다 – 참고: Fourie, Dehann, et al. “Towards Real-Time Non-Gaussian SLAM for Underdetermined Navigation.” (IROS 2020). ↩

  4. 여기서 예측하는 대상을 variable, 그 관계에 대해 factor 라고 부른다. factor 는 수학적으로는 n-ary function이다. 자세한 내용은 이 책8 의 Chapter 1장 (만 읽어도 됨) 참고. ↩

  5. 더 알아보고싶다면, 이 논문을 참고. Grisetti, Giorgio, et al. “Least squares optimization: From theory to practice.” Robotics (2020) ↩

  6. 그래서 SLAM이 왕왕 iterative non-linear least-square optimization 이라고 불리기도 한다 ↩

  7. Dellaert, Frank, and Michael Kaess. “Factor graphs for robot perception.” Foundations and Trends in Robotics (2017) ↩ ↩2 ↩3

  8. SLAM system matrix figure 에서 $b$가 마치 measurement 값인것 처럼 일단 소개를 했었었다 (쉬운 이해를 위해). 하지만 사실 b는 prediction error vector이다. 즉 어떤 시점 $i$ 에서, measurement model 을 이용해서 예측된 (우리가 그 값일 거라고 기대하는) measurement $h_{i}(X_{i}^{o})$ 와 실제로 얻은 measurement 값 $z_{i}$ 의 차이가 $b$ vector 가 된다. 즉, $|z_{i} - h_{i}(X_{i}^{o})|$ 가 $b$ vector인 것이다. 더 엄밀하게는 prediction error vector에 whitening 까지 된 것이 $b$ vector가 되는 것인데, 자세한 내용은 Factor Graph Book8 의 챕터 2.3 을 참고. ↩


Home Top

Giseop Kim , 2022 — built with Jekyll using Lagom theme